Equazioni irrazionali
In questa sezione sono contenuti esercizi sulle equazioni irrazionali. Esistono varie tipologie di equazioni irrazionali e in questa sezione analizziamo come risolverle.
1 Tipo
![]() con
con ![]()
Per risolvere questo tipo di equazione procediamo nel seguente modo:
![]()
![]()
| Numero | Esercizio | |
|---|---|---|
| 1 | svolgimento | |
| 2 | svolgimento | |
| 3 | svolgimento |
2 Tipo
Un secondo tipo di equazioni irrazionali ha anche al secondo membro dell’uguaglianza un polinomio in x.
![]()
Per risolvere questa equazione dobbiamo impostare un sistema per soddisfare due condizioni: la prima serve per garantire che il secondo membro sia positivo o al più pari a zero (in quanto al primo membro c’è una radice quadrata), mentre la seconda condizione permette di risolvere l’equazione elevando entrambi i membri al quadrato.
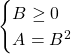
| Numero | Esercizio | |
|---|---|---|
| 1 | svolgimento | |
| 2 | svolgimento | |
| 3 | svolgimento | |
| 4 | svolgimento | |
| 5 | svolgimento |