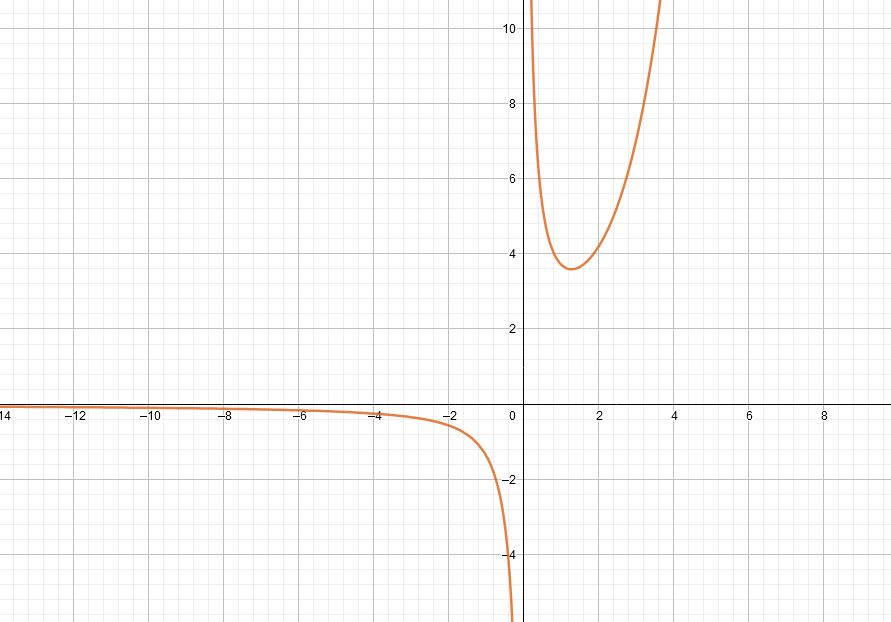
Studio di funzione esponenziale – Esercizio 3

17 Novembre 2019 gpalmieri Funzioni

Studiare la seguente funzione esponenziale (studio di funzione esponenziale):

$f(x)=\frac{e^x+1}{x}$

Dominio

Per prima cosa individuiamo il dominio della funzione cioè l’insieme dei valori che hanno una associazione con un valore nel codominio della funzione. Per trovare il dominio è necessario classificare la funzione. La funzione è razionale fratta e anche esponenziale. Per i fatto che è una funzione fratta, dobbiamo imporre che il denominatore della frazione sia diverso da zero:

$x \neq 0$

Il numeratore non pone problemi per il dominio in quanto è un esponenziale sommato ad un valore numerico. Concludiamo quindi che il dominio è il seguente intervallo di valori:

$D: (-\infty;0) \cup (0;+\infty)$

Intersezioni con gli assi

Il secondo problema da risolvere è quello di individuare leintersezioni della funzioni con gli assi coordinati. Per trovare le intersezioni è necessario risovere due sistemi:

Asse x

$\begin{cases}y=0\\ \frac{e^x+1}{x}=0 \end{cases}$

$\begin{cases}y=0\\ e^x+1=0 \end{cases}$

$\begin{cases}y=0\\ e^x=-1 \end{cases}$

$e^x=-1$

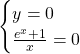
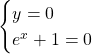
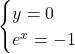
Questa ultima equazione non è risolvibile in quanto un’ esponenziale non può essere mai un valore negativo, ovvero non può esistere nessun valore che sostituito alla variabile x fa diventare una potenza un valore negativo. Concludiamo quindi che non ci sono intersezioni con l’asse x.

Asse y

$\begin{cases}x=0\\ \y=frac{e^x+1}{x} \end{cases}$

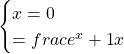
Dovremmo risolvere questo sistema per sostituzione sostituendo al posto della x della seconda equazione il valore 0. Non procediamo e non facciamo questa operazione perchè sappiamo che il valore 0 non appartiene al dominio. Se procedessimo infatti troveremmo un denominatore nullo. Concludiamo che non ci sono intersezioni con l’asse y.

Segno

Lo studio del segno ci permetterà di trovare l’insieme di positività (ovvero per quali valori del dominio la funzione è positiva) e quello di negatività. Per risolvere questo problema poniamo la funzione maggiore di zero:

$\frac{e^x+1}{x}>0$

Essendo una frazione troviamo il segno del numeratore, poi quello del denominatore e infine effettuiamo il prodotto dei segni:

$N: e^x+1 > 0$

$e^x >-1 -> \forall x \in R$

Il numeratore è sempre positivo (un esponenziale positivo sommato ad un numero positivo non può che essere un numero positivo!)

$D: x > 0$

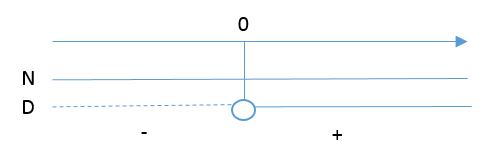
La funzione è quindi negativa per i valori precedenti allo zero e positiva per quelli successivi:

Limiti

Studiamo ora i limiti della funzione agli estremi del dominio:

1 Limite

$\lim_{x\to -\infty} \frac{e^x+1}{x}$

$\frac{e^{-\infty}+1}{(-\infty)}$

$\frac{0+1}{-\infty}$

Un numero fratto infinito nella teoria dei limiti è 0 quindi:

$\lim_{x\to -\infty} \frac{e^x+1}{x} = 0$

2 Limite

$\lim_{x\to 0^{-}} \frac{e^x+1}{x}$

$\frac{e^{0^{-}}+1}{0^{-}}$

$\frac{1+1}{0}$

Un numero fratto zero nella teoria dei limiti è \infty quindi:

$\lim_{x\to 0^{-}} \frac{e^x+1}{x} = -\infty$

3 Limite

$\lim_{x\to 0^{+}} \frac{e^x+1}{x} = +\infty$

4 Limite

$\lim_{x\to +\infty} \frac{e^x+1}{x}$

$\frac{e^{+\infty}+1}{(+\infty)}$

$\frac{+\infty}{+\infty}$

che è una forma indeterminata. Per risolvere l’indeterminatezza di questa forma ricordiamo che l’esponenziale tende all’infinito più velocemente di una potenza quindi il limite è infinito in quanto il denominatore è “più veloce” del denominatore.