Serie Numeriche
Criterio di Cauchy
Condizione necessaria e sufficiente affinché ![]() sia convergente é che
sia convergente é che ![]() tale che
tale che
![]() per ogni
per ogni ![]() e per ogni
e per ogni ![]()
Possiamo iniziare ora ad enunciare i criteri per la convergenza di una serie a termini non negativi.
Primo criterio del Confronto (o di Gauss)
Siano ![]() e
e ![]() due serie a termini non negativi, e sia
due serie a termini non negativi, e sia ![]() , allora:
, allora:
- se
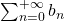 converge, allora
converge, allora 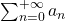 converge,
converge, - se
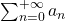 diverge, allora
diverge, allora 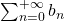 diverge.
diverge.
Definizione
Due serie ![]() e
e ![]() si dicono asintoticamente equivalenti se
si dicono asintoticamente equivalenti se
![]()
e si scrive ![]() per
per ![]() .
.
Secondo criterio del Confronto (Versione Asintotica)
Siano ![]() e
e ![]() due serie a termini non negativi. Sia
due serie a termini non negativi. Sia ![]() e
e ![]() , tali che esista il limite
, tali che esista il limite
![]() , allora
, allora
- se
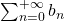 converge, allora
converge, allora 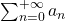 converge,
converge, - se
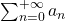 diverge, allora
diverge, allora 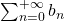 diverge.
diverge.
Se inoltre ![]() possiamo ricondurre il limite sempre al volore
possiamo ricondurre il limite sempre al volore ![]() con semplici tecniche algebriche, quindi abbiamo che
con semplici tecniche algebriche, quindi abbiamo che ![]() per
per ![]() . In questo caso le due serie hanno lo stesso carattere..
. In questo caso le due serie hanno lo stesso carattere..
Criterio della radice
Sia ![]() una serie a termini non negativi. Supponiamo che
una serie a termini non negativi. Supponiamo che
![]() , allora la serie
, allora la serie ![]()
- converge se
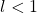 ,
, - diverge se
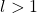 ,
, - non possiamo concludere nulla sul comportamento della serie se
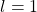 .
.
Criterio del rapporto
Sia ![]() una serie a termini non negativi. Supponiamo che
una serie a termini non negativi. Supponiamo che
![]() , allora la serie
, allora la serie ![]()
- converge se
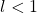 ,
, - diverge se
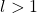 ,
, - non possiamo concludere nulla sul comportamento della serie se
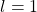 .
.
Criterio degli infinitesimi
Sia ![]() una serie a termini non negativi. Supponiamo che esista
una serie a termini non negativi. Supponiamo che esista ![]() , con
, con ![]() e
e ![]() , allora se
, allora se
 e
e 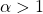 allora
allora 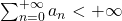 ,
, e
e  allora
allora  .
.
Esempio 8 (La serie armonica)
![]()
Per studiare il carattere della seguente serie consideriamo il limite notevole:
![]()
Poiché ![]() è crescente allora abbiamo che
è crescente allora abbiamo che ![]()
![]()
Utilizziamo il criterio del confronto di Gauss dove ![]() e
e ![]()
Poichè ![]() e
e ![]() diverge (esempio 4) allora anche
diverge (esempio 4) allora anche ![]() diverge.
diverge.
![]() la serie
la serie ![]() diverge positivamente.
diverge positivamente.
Esempio 9 (La serie armonica generalizzata di ordine ![]() )
)
![]() con
con ![]() .
.
Studiamo il carattere della seguente serie al variare di ![]() .
.
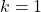 la serie si riduce alla serie armonica e diverge.
la serie si riduce alla serie armonica e diverge.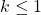 la serie diverge, infatti il termine generale
la serie diverge, infatti il termine generale 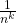 non è infinitesima per
non è infinitesima per 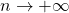 , pertanto non è soddisfatta la condizione necessaria affinchè la serie converga.
, pertanto non è soddisfatta la condizione necessaria affinchè la serie converga.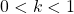 la serie diverge. Utilizziamo il metodo del confronto di Gauss. Abbiamo
la serie diverge. Utilizziamo il metodo del confronto di Gauss. Abbiamo 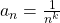 e consideriamo
e consideriamo 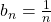 , dunque
, dunque 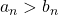 e poichè
e poichè 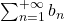 diverge allora anche
diverge allora anche 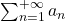 diverge.
diverge.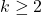 la serie converge. Utilizziamo ancora il metodo del confronto di Gauss. Sia
la serie converge. Utilizziamo ancora il metodo del confronto di Gauss. Sia 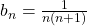 è il termine generale della serie Mengoli che abbiamo già viso che converge, dunque anche
è il termine generale della serie Mengoli che abbiamo già viso che converge, dunque anche 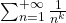 per
per 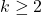 converge poiché
converge poiché 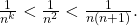
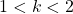 la serie converge. Per questo punto è necessario l’uso di un altro Criterio.
la serie converge. Per questo punto è necessario l’uso di un altro Criterio.
Criterio Integrale per le serie
Se ![]() è decrescente e
è decrescente e ![]() , allora
, allora
![]() converge, se e solo se
converge, se e solo se ![]() converge.
converge.
Consideriamo dunque ![]() con
con ![]() .
.
Abbiamo già visto che per ![]() la serie diverge, dunque consideriamo
la serie diverge, dunque consideriamo
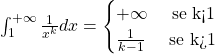 .
.
Definizione. (Convergenza Assoluta)
Una serie ![]() si dice assolutamente convergente se
si dice assolutamente convergente se ![]() .
.
Teorema.
Una serie assolutamente convergente è convergente.
SERIE A TERMINI ALTERNI
Una serie a termini alterni è del tipo ![]() cioè
cioè ![]() .
.
Criterio di Leibniz
Sia data la serie ![]() con
con ![]() per ogni
per ogni ![]() . Se
. Se ![]() è una successione decrescente ed infinitesima, allora la serie
è una successione decrescente ed infinitesima, allora la serie ![]() è convergente.
è convergente.
Esempi.
10. ![]() . Verifichiamo se sia soddisfatta la condizione necessaria per la convergenza della serie.
. Verifichiamo se sia soddisfatta la condizione necessaria per la convergenza della serie.
![]() quindi è soddisfatta!
quindi è soddisfatta!
Possiamo scrivere ![]() .
.
E quindi abbiamo una serie telescopica, dove
![]()
![]()
![]()
![]()
![]()
11. ![]() .
.
Osserviamo che il termine generale della serie ![]() è infinitesimo e decrescente, dunque per il criterio di Leibniz le serie converge.
è infinitesimo e decrescente, dunque per il criterio di Leibniz le serie converge.