Determinante di una matrice
Il determinante è un numero che viene associato ad una matrice quadrata. Non ha senso quindi parlare di determinante di una matrice che non sia quadrata. Ricordiamo che per definizione una matrice si dice quadrata quando ha lo stesso numero di righe e di colonne. L’ordine di una matrice quadrata è il numero di righe e di colonne che essa possiede. Il simbolo che indica il determinante della matrice sono due linee dritte fra gli elementi della matrice.
Vediamo come è possibile ora calcolare il determinante di una matrice.
Primo ordine
Il determinante di una matrice del primo ordine è uguale al numero stesso che compare nella matrice
![]()
Secondo ordine
Il determinante di una matrice del secondo ordine è uguale alla differenza fra il prodotto dei due elementi della diagonale principale e il prodotto dei due elementi della diagonale secondaria.
![]()
Vediamo un esempio concreto:
![]()
Terzo ordine
Se la matrice quadrata ha ordine 3 possiamo calcolare il determinante attraverso il metodo di Sarrus o Laplace.
Sarrus
Laplace
Laplace ha ideato un metodo per il calcolo del determinante che è ricorsivo. Data una matrice quadrata A di ordine n e di elementi ![]() si definisce:
si definisce:
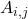 la sottomatrice quadrata che si ottiene eliminando dalla matrice A la riga i e la colonna j
la sottomatrice quadrata che si ottiene eliminando dalla matrice A la riga i e la colonna j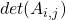 , minore complementare dell’elemento
, minore complementare dell’elemento 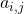
- il valore
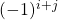 cofattore dell’elemento
cofattore dell’elemento 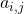
Il primo teorema di Laplace dice che per calcolare il determinante di una matrice dobbiamo sommare tutti i cofattori degli elementi di una riga o colonna qualsiasi.
![]()
Vediamo un esempio pratico:
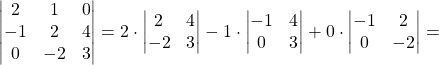
![]()
![]()
Prosegui con gli esercizi.
Torna a matrici
Torna a operazioni fra matrici
Vai a calcolo del rango
