Serie Numeriche
SERIE A TERMINI NON NEGATIVI
Diremo che una serie ![]() é una serie a termini non negativi se
é una serie a termini non negativi se ![]() risulta
risulta ![]() .
.
Mentre si dice che é una serie a termini positivi se ![]() .
.
La successione ![]() delle somme parziali di una serie a termini non negativi é crescente. Infatti poiché
delle somme parziali di una serie a termini non negativi é crescente. Infatti poiché ![]() allora
allora ![]() . Quindi
. Quindi ![]() non può essere indeterminata, ma ammette sicuramente limite.
non può essere indeterminata, ma ammette sicuramente limite.
Esempio 6. (La serie geometrica)
![]()
![]() si dice ragione della serie geometrica.
si dice ragione della serie geometrica.
Utilizzando il principio di induzione si può mostrare che ![]()
Il ![]() varia rispetto al valore di
varia rispetto al valore di ![]() .
.
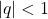 cioè
cioè 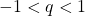 allora
allora 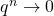 per
per 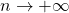 e quindi
e quindi
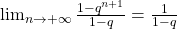
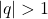 cioè
cioè 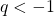 e
e 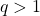 allora
allora 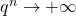 per
per 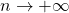
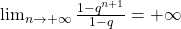 , perciò la serie diverge.
, perciò la serie diverge.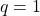 allora
allora 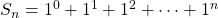 ,
,
dunque la serie diverge.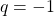 allora
allora 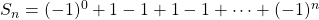 ,
,
dunque la serie si riduce al caso della serie alternata che è indeterminata.
La serie geometrica di ragione ![]() :
:
- converge se
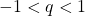 a
a 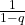
- diverge se
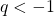 e
e 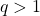
- è irregolare se
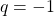
Esempio 7.
![]()
Tale serie converge, infatti é una serie geometrica di ragione
![]() dove
dove ![]() , e converge alla somma
, e converge alla somma ![]()