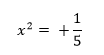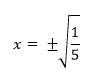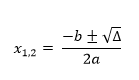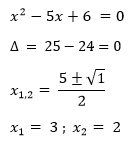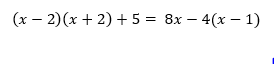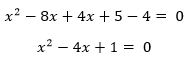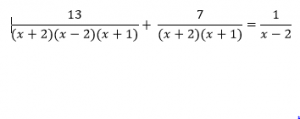Equazioni Secondo Grado
Definizione
Un’equazione intera in un’incognita x, dopo aver svolto le opportune semplificazioni, si può scrivere in questa forma normale:
![]()
dove è un polinomio di grado n in x. Se il polinomio è di secondo grado l’equazione si dice di secondo grado o quadratica. La forma con la quale possiamo scrivere l’equazione è la seguente:
L’equazione si dice completa quando sono presenti tutti i termini a, b e c. L’equazione si dice incompleta pura quando manca il termine b e incompleta spuria quando manca il termine c. Se mancano sia b che c si dice monomia.
Equazioni Pure
Esempi
Come si risolve?
La logica per risolvere un’equazione di secondo grado pura è quella di isolare l’incognita x. Per “isolare” si intende far sì che al primo membro ci sia solo l’incognita. Questo procedimento consiste nel fare vari passaggi applicando il primo e il secondo principio delle equazioni.
La prima cosa che dobbiamo fare con questa equazione è quella di spostare il termine numerico 1 che si trova al primo membro, al secondo membro.
Poi dobbiamo eliminare quel 5 che sta davanti alla perché abbiamo detto che al primo membro ci deve essere solo l’incognita.
A questo punto, poiché finalmente al primo membro abbiamo solo l’incognita, possiamo porre sotto radice quadrata primo e secondo membro. Al primo membro rimane la x mentre al secondo le due soluzioni:
Equazioni Spurie
Esempi
![]()
Come si risolve?
La logica per risolvere un’equazione di secondo grado spuria è quella di mettere in evidenza in termine in x e si otterrà un prodotto di due termini uno è il monomio x e l’altro un binomio. In definitiva questa espressione letterale sarà uguale a zero quando il monomio x è 0 oppure anche quando l’espressione di primo grado è uguale a zero.
![]()
La prima cosa che dobbiamo fare è mettere in evidenza la x:
![]()
le soluzioni saranno quindi:
![]()
e
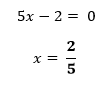 Equazioni Complete
Equazioni Complete
Esempi
![]()
Come si risolve?
Un equazione di secondo grado completa si risolve utilizzando una formula di risoluzione ben definita. Per prima cosa si calcola il
dal Δ possiamo capire il numero di soluzioni dell’equazione:
Le soluzioni si possono calcolare con questa formula:
Risoluzione Equazione Complessa
Ci chiediamo ora come risolvere un’equazione complessa che non si presenta a prima vista nelle forme che abbiamo considerato precedentemente. Come vedremo dovremo fare vari passaggi che sono in definitiva sempre gli stessi.
Se l’equazione si presenta in questa forma la prima cosa che dobbiamo notare e che non è fratta in quanto l’incognita non è contenuta al denominatore.
- mcm denominatori
bisogna portare tutto sotto lo stesso denominatore per poi eliminarli nel passaggio successivo. In questo caso i fattori sono:
- 20 = 5*2
- 5
Il minimo comune multiplo è 5*2 quindi 20
- eliminare i denominatori
- semplificare
in questo passaggio si svolgono tutti i prodotti facendo attenzione alla presenza di prodotti notevoli che si possono risolvere secondo le regole che conosciamo.
![]()
- ordinare
portiamo tutti i termini al primo membro e ordiniamo in maniera decrescente le incognite in x (quindi a partire dal grado 2 a decrescere):
A questo punto abbiamo portato l’equazione ad una forma che conosciamo e possiamo risolverla secondo le tecniche analizzate precedentemente.
Risoluzione Equazione Fratta
In una equazione letterale fratta al denominatore compare anche l’incognita x. Il procedimento rimane lo stesso del caso precedente ma si aggiungono alcuni passaggi da considerare prima di tutti gli altri.
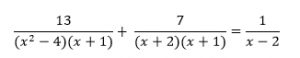
- fattorizzare denominatori
il primo passaggio in questo caso e quello della fattorizzazione dei denominatori. Questo passaggio ci consentirà di individuare bene quali sono i fattori da considerare nel minimo comune multiplo. Quello che notiamo nell’esempio e che al primo denominatore è presente una somma per differenza che si può sviluppare nel seguente modo:
- mcm denominatori
possiamo ora individuare il minimo comune multiplo dei denominatori ricordando che un polinomio si considera come un unico fattore:
- (x + 2)
- (x – 2)
- (x + 1)
Prenderò quindi tutti e tre i fattori
(x+2)(x-2)(x+1)
- eliminare i denominatori
per eliminare i denominatori sarà prima necessario individuare il campo di esistenza degli stessi e cioè escludere tutti i valori delle x che li annullano:
Dopo aver eliminato i denominatori si procede come indicato nel caso precedente.