Esercizio – Studio di funzione fratta

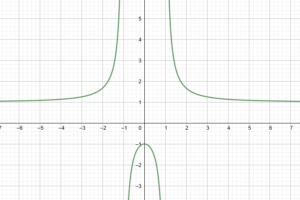
20 Gennaio 2020 gpalmieri Equazioni con valore assoluto, Funzioni Razionali Fratte

Studiare la seguente funzione razionale fratta (studio di funzione fratta):

$f(x)=\frac{x^2+1}{x^2-1}$

Dominio

Per prima cosa individuiamo il dominio della funzione cioè l’insieme dei valori che hanno una associazione con un valore nel codominio della funzione. Per trovare il dominio è necessario classificare la funzione. La funzione è razionale fratta per questo dobbiamo escludere tutti i valori che annullano il denominatore in quanto una frazione non può avere un denominatore uguale a zero. Ciò corrisponde a questa espressione:

$x^2-1 \neq 0$

Per risolvere ricordiamo la regola del prodotto notevole somma per differenza:

$(x-1) \cdot (x+1) \neq 0$

$x \neq 1$

$x \neq -1$

Concludiamo quindi che il dominio è il seguente intervallo di valori:

$D: (-\infty;-1) \cup (-1;1) \cup (1;+\infty)$

Intersezioni con gli assi

Il secondo problema da risolvere è quello di individuare le intersezioni della funzioni con gli assi coordinati. Per trovare le intersezioni è necessario risovere due sistemi:

Asse x

$\begin{cases}y=0\\ \frac{x^2+1}{x^2-1}=0 \end{cases}$

$\begin{cases}y=0\\ x^2+1=0 \end{cases}$

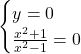
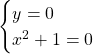
Questa ultima equazione non è risolvibile in quanto un numero positivo (perchè al quadrato) sommato con 1 non può mai essere pari a 0. Concludiamo quindi che non ci sono intersezioni con l’asse x.

Asse y

$\begin{cases}x=0\\ \y=\frac{x^2+1}{x^2-1} \end{cases}$

$\begin{cases}x=0\\ \y=\frac{0+1}{0-1} \end{cases}$

$\begin{cases}x=0\\ \y=-1 \end{cases}$

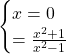
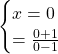
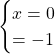
E’ presente un punto di intersezione: $P(0,-1)$

Segno

Lo studio del segno ci permetterà di trovare l’insieme di positività (ovvero per quali valori del dominio la funzione è positiva) e quello di negatività. Per risolvere questo problema poniamo la funzione maggiore di zero:

$\frac{x^2+1}{x^2-1}>0$

Essendo una frazione troviamo il segno del numeratore, poi quello del denominatore e infine effettuiamo il prodotto dei segni:

$N: x^2+1 > 0 \forall x \in R$

Il numeratore è sempre positivo (un numero al quadrato sommato ad un numero positivo non può che essere un numero positivo!)

$D: x^2-1 > 0$

$(x-1)(x+1) > 0$

$x>1$

$x>-1$

La funzione è positiva da $-\infty$ fino a $-1$ e da $1$ a $\infty$

Limiti

Studiamo ora i limiti della funzione agli estremi del dominio:

1 Limite

$\lim_{x\to -\infty} \frac{x^2+1}{x^2-1}$

$\frac{(-\infty)^2+1}{(-\infty)^2-1}$

$\frac{\infty}{\infty}$

Questa è una forma indeterminata. Poichè sia al numeratore che al denominatore compaiono due polinomi possiamo mettere in evidenza il termine con grado maggiore:

$\lim_{x\to -\infty} \frac{x^2(1+\frac{1}{x^2}}{x^2(1+\frac{1}{x^2}}$

Semplificando il tutto scopriamo che:

$\lim_{x\to -\infty} \frac{x^2+1}{x^2-1}=1$

2 Limite

$\lim_{x\to -1^{-}} \frac{x^2+1}{x^2-1}$

$\lim_{x\to -1^{-}} \frac{(-1)^2+1}{(-1^{-})^2-1}$

$\lim_{x\to -1^{-}} \frac{(-1)^2+1}{0^{+}} = +\infty$

3 Limite

$\lim_{x\to -1^{+}} \frac{x^2+1}{x^2-1}$

$\lim_{x\to -1^{+}} \frac{(-1)^2+1}{1^{+}-1}$

$\lim_{x\to -1^{+}} \frac{(-1)^2+1}{0^{-}} = -\infty$

4 Limite

$\lim_{x\to 1^{-}} \frac{x^2+1}{x^2-1} = -\infty$

5 Limite

$\lim_{x\to 1^{+}} \frac{x^2+1}{x^2-1} = +\infty$

6 Limite

$\lim_{x\to +\infty} \frac{x^2+1}{x^2-1} = 1$

Asintoti

Dallo studio dei limiti troviamo un asintoto orizzontale in quanto:

$\lim_{x\to \pm\infty} \frac{x^2+1}{x^2-1} = 1$

Quindi la retta $y=1$ è asintoto orizzontale.

Sono presenti anche due asintoti verticali in quanto:

$\lim_{x\to -1} \frac{x^2+1}{x^2-1} = \infty$

$\lim_{x\to 1} \frac{x^2+1}{x^2-1} = \infty$

Quindi le rette $x=-1$ e $x=1$ sono asintoti verticali.

Derivata 1

$f(x)=\frac{x^2+1}{x^2-1}$

Per calcolare la derivata applichiamo la regola che si applica alle funzioni fratte:

$d[\frac{f(x)}{g(x)}] = \frac{f^{'}(x) g(x)-f(x)g^{'}(x)}{[g(x)]^2}$

$f(x) = \frac{2x(x^2-1) - 2x(x^2+1)}{(x^2-1)^2}$

$f(x) = \frac{2x[(x^2-1) - (x^2+1)]}{(x^2-1)^2}$

$f(x) = \frac{2x[x^2-1 - x^2 - 1)]}{(x^2-1)^2}$

$f(x) = \frac{2x[-2]}{(x^2-1)^2}$

$f(x) = \frac{-4x}{(x^2-1)^2}$

Studiamo ora il segno della derivata prima per capire la monotonia della funzione ed individuare i sui punti stazionari:

$\frac{-4x}{(x^2-1)^2} \geq 0$

$N: -4x \geq 0$

$4x \leq 0$

$x \leq 0$

$D: (x^2-1)^2 > 0 \forall x \in R$

La funzione è crescente prima di 0 e decrescente dopo lo 0. Infine in 0 è presente un punto di massimo, possiamo trovare la coordinata y del punto sostituendo il valore nella funzione:

$f(0) = \frac{1}{-1} = -1$

Il massimè è $M(0,-1)$

Torna a studio di funzioni razionali fratte

Torna a matematica

Comments

comments

Lascia un commento funzione fratta, news, studio funzione

L	M	M	G	V	S	D
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31