Esercizio 5 – Intersezioni con gli assi
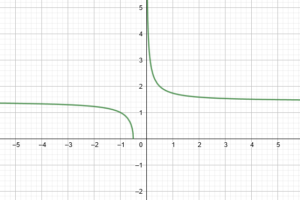
Trova le intersezioni con gli assi della seguente funzione irrazionale e fratta
![]()
Per risolvere il problema delle intersezioni con gli assi coordinati dobbiamo svolgere due sistemi:
Asse x
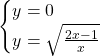
![Rendered by QuickLaTeX.com \[\begin{cases}y=0\\\sqrt{\frac{2x-1}{x}}=0\end{cases}\]](https://www.eserciziario.eu/wp-content/ql-cache/quicklatex.com-526e0854a5740c8c9ad506d3fc9575d4_l3.png)
Dobbiamo quindi risolvere la seguente equazione fratta:
![]()
Sappiamo che questa radice si annulla se l’argomento si annulla si annulla quindi:
![]()
A sua volta questa frazione si annulla se il numeratore è nullo:
![]()
![]()
Possiamo concludere che il sistema ha una coppia di soluzione e quindi è presente un solo punto di intersezione con l’asse x:
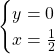
Asse y
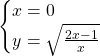
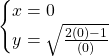
Questo sistema non si può risolvere perchè la x uguale a zero annullerebbe il denominatore. Il valore zero infatti non appartiene al dominio della funzione.
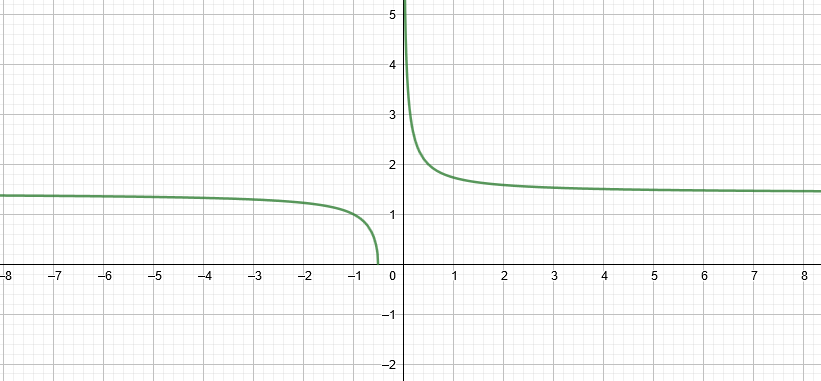
Il grafico mostra che quanto abbiamo studiato è corretto in quanto è presente un punto di intersezione con l’asse x e nessun punto di intersezione con l’asse y.
Torna a intesezioni con gli assi coordinati
Torna allo studio di funzioni