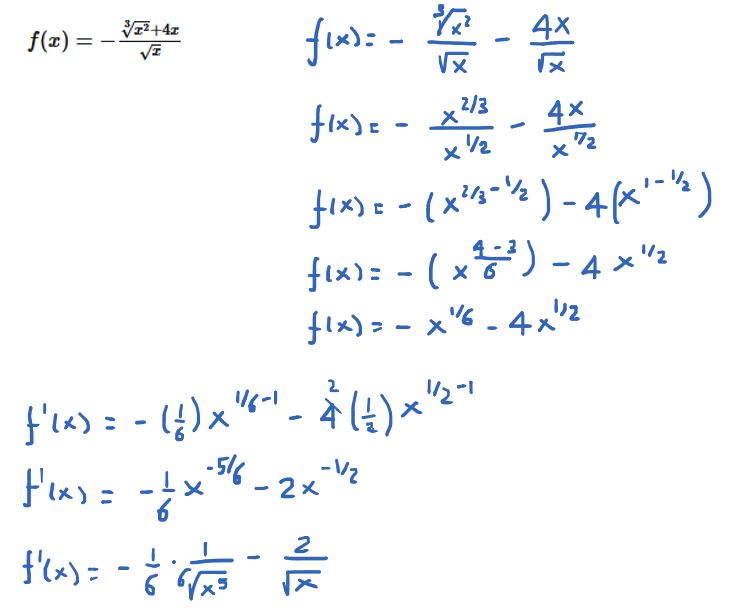Derivata della somma di funzioni – Esercizio 10

2 Gennaio 2019 gpalmieri Derivata della somma di funzioni

derivata della somma di funzioni esercizio 10

Anche le questa funzione appare noncome una somma di funzioni ma come una frazione, poichè al denominatore è presente un solo monomio possiamo dividere tutti i termini del denominatore per esso.

Per risolvere questo esercizio dobbiamo ricordare due regole fondamentali delle potenze:

$x^{-k} = \frac{1}{x^k}$

$\sqrt[s]{x^k} = x^{\frac{k}{s}}$

Prima di individuare la derivata conviene sempre riscrivere tutto il polinomio sotto forma di potenze del tipo $x^k$ per sfruttare semplicemente la regola di derivazione $d[x^k] = kx^{k-1}$

Comments

comments

Lascia un commento derivata somma funzioni

L	M	M	G	V	S	D
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30	31

Derivata della somma di funzioni – Esercizio 10

Comments

Lascia un commento Annulla risposta